deborda.org

The de Borda Institute, after Jean-Charles de Borda, 1733-99

Navigation

About us

I'm on my way to China again. And here's the blog: https://deborda.substack.com/p/debordaabroad2

-/-/-/-/-/-/-/-/-/-

The de Borda Institute

aims to promote the use of inclusive, multi-optional and preferential voting procedures, both in parliaments/congresses and in referendums, on all contentious questions of social choice.

This applies specifically to decision-making, be it for the electorate in regional/national polls, for their elected representatives in councils and parliaments, for members of a local community group, a company board, a co-operative, and so on. But we also cover elections.

* * * * *

The Institute is named after Jean-Charles de Borda, and hence the well-known voting procedure, the Borda Count BC; but Jean-Charles actually invented what is now called the Modified Borda Count, MBC - the difference is subtle:

In a vote on n options, the voter may cast m preferences; and, of course, m < n.

In a BC, points are awarded to (1st, 2nd ... last) preferences cast according to the rule (n, n-1 ... 1) {or (n-1, n-2 ... 0)} whereas,

in an MBC, points are awarded to (1st, 2nd ... last) preferences cast according to the rule (m, m-1 ... 1).

The difference can be huge, especially when the topic is controversial: the BC benefits those who cast only a 1st preference; the MBC encourages the consensual, those who submit not only a 1st preference but also their 2nd (and subsequent) compromise option(s). And if (nearly) every voter states their compromise option(s), an MBC can identify the collective compromise.

_/-_/-_/-_/-_/-_/-_/-_/-

DECISION-MAKER
Inclusive voting app

https://debordavote.com

THE APP TO BEAT ALL APPS, APPSOLUTELY!

(The latest in a long-line of electronic voting for decision-making; our first was in 1991.)

_/-_/-_/-_/-_/-_/-_/-_/-

FINANCES

The Institute was estabished in 1997 with a cash grant of £3,000 from the Joseph Rowntree Charitabe Trust, and has received the occasional sum from Northern Ireland's Community Relations Council and others. Today it relies on voluntary donations and the voluntary work of its board, while most running expenses are paid by the director.

_/-_/-_/-_/-_/-_/-_/-_/-

A BLOG

"De Borda abroad." From Belfast to Beijing and beyond... and back. Starting in Vienna with the Sept 2017 TEDx talk, I give lectures in Belgrade, Sarajevo, Istanbul, Tbilisi, Yerevan, Tehran, Beijing, Tianjin, Xuzhou, Hong Kong and Taiwan... but not in Pyongyang. Then back via Mongolia (where I had been an election observer in June 2017) and Moscow (where I'd worked in the '80s).

I have my little fold-up Brompton with me - surely the best way of exploring any new city! So I prefer to go by train, boat or bus, and then cycle wherever in each new venue; and all with just one plastic water bottle... or that was the intention!

The story is here.

In Sept 2019, I set off again, to promote the book of the journey. After the ninth book launch in Taipei University, I went to stay with friends in a little village in Gansu for the Chinese New Year. The rat. Then came the virus, lockdown... and I was stuck.

_/-_/-_/-_/-_/-_/-_/-_/-

The Hospital for Incurable Protestants

The Mémoire of a Collapsed Catholic

This is the story of a pacifist in a conflict zone, in Northern Ireland and the Balkans. Only in e-format, but only £5.15. Available from Amazon.

_/-_/-_/-_/-_/-_/-_/-

The director alongside the statue of Jean-Charles de Borda, capitaine et savant, in l’École Navale in Brest, 24.9.2010. Photo by Gwenaelle Bichelot.

Annual Reports

Decision-Maker APP

Won by One

MBC

QBS

The Matrix Vote

Practical Examples

WELCOME

Welcome to the home page of the de Borda Institute, a Northern Ireland-based international organisation (an NGO) which aims to promote the use of inclusive voting procedures on all contentious questions of social choice. For more information use the menu options above or feel free to contact the organisation's headquarters. If you want to check the meaning of any of the terms used, then by all means have a look at this glossary.

As shown in these attachments, there are many voting procedures for use in decision-making and even more electoral systems. This is because, in decision-making, there is usually only one outcome - a singe decision or a shopping ist, a prioritisation; but with some electoral systems, and definitely in any proportional ones, there can be several winners. Sometimes, for any one voters' profile - that is, the set of all their preferences - the outcome of any count may well depend on the voting procedure used. In this very simple example of a few voters voting on just four options, and in these two hypothetical examples on five, (word document) or (Power-point) in which a few cast their preferences on five options, the profiles are analysed according to different methodologies, and the winner could be any one of all the options. Yet all of these methodologies are called democratic! Extraordinary!

The electorate decides...

Let us assume that the ballots have been printed and distributed and that an electorate of five persons - Messrs J, K, L, M and N - have voted by giving a 1 to their first preference, a 2 to their second preference, and so on.

Let us imagine that they voted as follows:

Preferences	Ms. J	Mr. K	Ms. L	Mr. M	Ms. N
1^st	A	A	D	D	C
2^nd	B	B	B	B	B
3^rd	C	C	-	C	D
4^th	D	D	-	A	A

Please note that Ms L only gave her first and second preferences; but that, of course, is her prerogative and is accepted by the software package.

Determining the final results...

An analysis of the votes according to eight different voting methodologies is as follows:

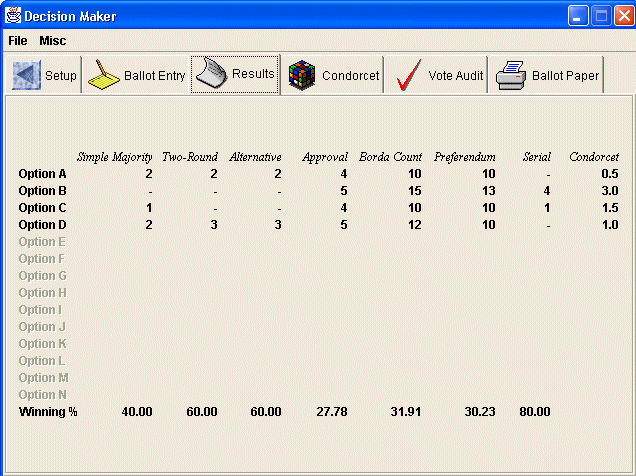
The methodologies are mentioned here and described in the analysis.

Majority (Plurality) Voting is used in most parliaments and most referendums.

Two-Round Voting is used in some referendums, eg, in New Zealand.

Approval Voting is sometimes used in the UN, though mainly as an electoral system.

Alternative Vote is used in Austraoian elections and, in its PR form, in elections in Ireland, North and South.

The Borda Count is a French methodology, used in part in Slovenian elections, to analyse the ethnic vote.

The Modified Borda Count, which is actually Jean-Charles de Borda's original formula, allows for partial voting in the Borda count.

Serial Voting is used in some Scandinavian parliaments, eg, in Sweden.

A Condorcet count is another French methodology.

All of these methodologies are described as democratic, yet in many instances, different counting procedures will lead to different results. In our own example, the ‘most popular’ options are:

VOTING PROCEDURE	WINNER(S)	RUNNER(S)-UP
Plurality Voting	A and D =
Two-round voting	D	A
Alternative Vote (AV) or STV	D	A
Approval Voting	B and D =
Borda Count (BC)	B	D
Modified Borda Count (MBC) or Preferendum	B	A, C and D =
SerialVoting	B	C
Condorcet	B	C

In analysing the vote, we must examine each methodology in turn. But first, we repeat the voters' profile, like this:

Preferences	Ms. J	Mr. K	Ms. L	Mr. M	Ms. N
1^st	A	A	D	D	C
2^nd	B	B	B	B	B
3^rd	C	C		C	D
4^th	D	D		A	A

or in a slightly different style.

	Preferences of:
Options	Ms. J	Mr. K	Ms. L	Mr. M	Ms. N
A	1^st	1^st	-	4^th	4^th
B	2^nd	2^nd	2^nd	2^nd	2^nd
C	3^rd	3^rd	-	3^rd	1^st
D	4^th	4^th	1^st	1^st	3^rd

Majority (Plurality) Voting considers only the first preferences, so while two people consider option A to be the best, and hence its score of two, the fact that two other people think it is the worst is not taken into account.

Two-Round Voting takes the two leading options from the plurality vote, and takes a straight majority vote between the two. Messrs J and K prefer A to D but Messrs L, M and N all prefer D to A, so D wins by 3 to 2.

In the Alternative Vote, option B is again (as in the plurality vote) considered to be the worst with a score of 0. Option C is the next least popular, and when its vote is transferred according to Mr. M's preferences, it goes to D. So D wins.

In Approval Voting, any preference expressed is regarded as a mark of approval, so in this analysis Options B and D gain the maximum score of 5 approvals.

A Borda Count is a straight points system with, in this instance, 4 points for a first preference, 3 for a second, and so on. And B wins.

In a Borda Preferendum, a partial vote is given a correspondingly partial score but, in this instance, the winner is still B.

Serial Voting considers the four options as if on an axis, and takes a majority vote between the two extremes first: A v D. A loses, so its then B v D. B wins this vote, so it's then B v C and again, B is the winner.

A Condorcet count is a series of pairings - A v B, A v C, A v D, B v C, B v D and C v D; the options which wins the most pairings is the winner and, in our example, it is again B.

This work is licensed under a Creative Commons License.